lcfoki.blogg.se

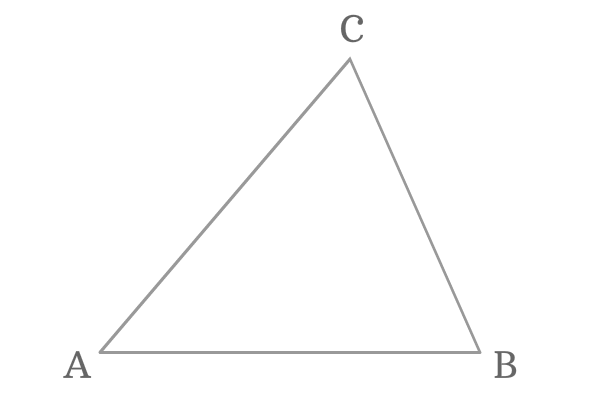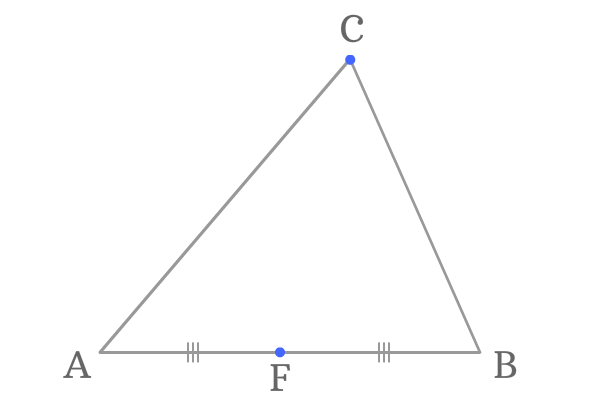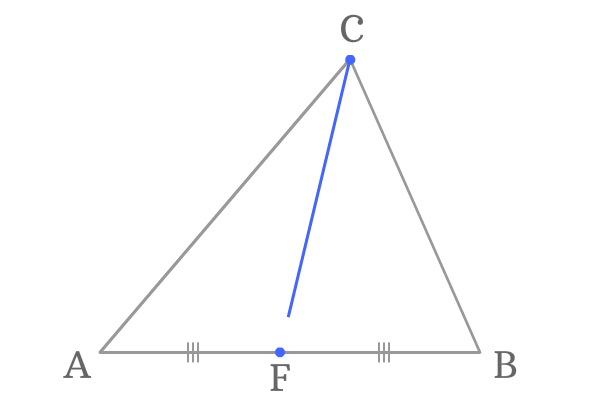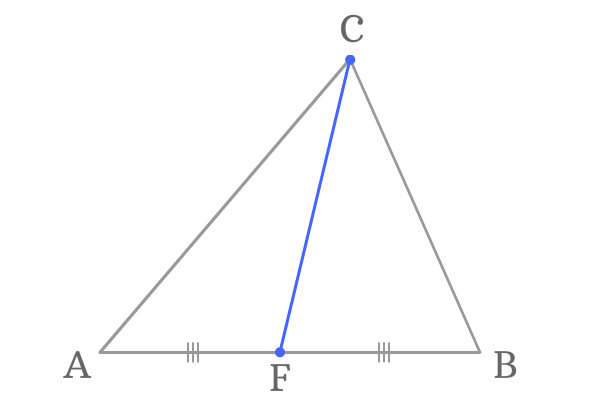
Weisstein, Eric W., " Triangle Median", MathWorld. In geometry, a median of a triangle is a line segment joining a vertex to the midpoint of the opposite side, thus bisecting that side.Constructing a median of a triangle with compass and straightedge animated demonstration.Medians of a triangle With interactive animation.Area of Median Triangle at cut-the-knot.Medians and Area Bisectors of a Triangle.↑ Leung, Kam-tim and Suen, Suk-nam "Vectors, matrices and geometry", Hong Kong University Press, 1994, pp.↑ Benyi, Arpad, "A Heron-type formula for the triangle", Mathematical Gazette 87, July 2003, 324–326.↑ Boskoff, Homentcovschi, and Suceava (2009), Mathematical Gazette, Note 93.15. The median of a triangle is the line connecting the top of the triangle to the middle of the opposite side.↑ 5.0 5.1 Posamentier, Alfred S., and Salkind, Charles T., Challenging Problems in Geometry, Dover, 1996: pp.E., "Halving a triangle," Mathematical Gazette 56, May 1972, 105-108. Triangles Geometry (all content) Math Khan Academy Geometry (all content) Unit: Triangles About this unit You probably like triangles. There are four medians, and they are all concurrent at the centroid of the tetrahedron. A line segment joining a vertex of a tetrahedron with the centroid of the opposite face is called a median of the tetrahedron. Let D be the midpoint of A B ¯ TetrahedronĪ tetrahedron is a three-dimensional object having four triangular faces. (Any other lines which divide the area of the triangle into two equal parts do not pass through the centroid.) The three medians divide the triangle into six smaller triangles of equal area.Ĭonsider a triangle ABC. So its equal to 2/3 times 15, which is equal to 10. And we could do it for any of the medians. Thus the object would balance on the intersection point of the medians.Įach median divides the area of the triangle in half hence the name, and hence a triangular object of uniform density would balance on any median. We proved that in a previous video, that the centroid is 2/3 along the way of any of these medians. 3 Formulas involving the medians' lengthsĮach median of a triangle passes through the triangle's centroid, which is the center of mass of an object of uniform density in the shape of the triangle.